物理 公式和定理总结
1. 水的分解:2H2O(l) -> 2H2(g) + O2(g)
2. 酸碱中和反应:HCl(aq) + NaOH(aq) -> NaCl(aq) + H2O(l)
3. 金属与非金属的单质反应:2Na(s) + Cl2(g) -> 2NaCl(s)
4. 燃烧反应:C3H8(g) + 5O2(g) -> 3CO2(g) + 4H2O(g)
5. 化学平衡反应:N2(g) + 3H2(g) -> 2NH3(g)
6. 沉淀反应:AgNO3(aq) + NaCl(aq) -> AgCl(s) + NaNO3(aq)
7. 氧化还原反应:2Mg(s) + O2(g) -> 2MgO(s)
8. 分解反应:2H2O2(aq) -> 2H2O(l) + O2(g)
9. 双替换反应:HCl(aq(aq) + NaOH(aq) -> NaCl(aq) + H2O(l)
10. 反应速率相关反应:2NO2(g) + F2(g) -> 2NO2F(g)
11. 酸催化酯化反应:CH3COOH(aq) + C2H5OH(aq) -> CH3COOC2H5(aq) + H2O(l)
12. 烷烃燃烧反应:C6H14(g) + 19O2(g) -> 6CO2(g) + 7H2O(g)
13. 酸碱滴定反应:HCl(aq) + NaOH(aq) -> NaCl(aq) + H2O(l)
14. 碳酸盐分解反应:CaCO3(s) -> CaO(s) + CO2(g)
15. 酸碱中和气体生成反应:HCl(g) + NH3(g) -> NH4Cl(s)
16. 高锰酸钾氧化亚硫酸钠反应:2KMnO4(aq) + 5Na2SO3(aq) + 8H2O(aq) -> K2SO4(aq(aq) + 2MnSO4(aq) + 2NaOH(aq)
17. 氧化还原反应:Cu(s) + 2AgNO3(aq) -> Cu(NO3)2(aq) + 2Ag(s)
18. 硫酸与钠氢化合物反应:H2SO4(aq) + 2NaOH(s) -> Na2SO4(aq) + 2H2O(l)
19. 醋酸酯水解反应:CH3COOC2H5(aq) + H2O(l) -> CH3COOH(aq) + C2H5OH(aq)
20. 燃烧反应:C4H10(g) + 6O2(g) -> 4CO2(g) + 5H2O(g)
21. 多元醇酸酐反应:C6H10O6(aq) + C4H6O3(aq) -> C10H16O8(aq) + H2O(l)
22. 气体与金属氧化物反应:3CO(g) + Fe2O3(s) -> 2Fe(s) + 3CO2(g)
物理板块
1. 速度公式:v = d/t (v为速度,d为距离,t为时间)
2. 加速度公式:a = (v - u)/t (a为加速度,v为末速度,u为初速度,t为时间)
3. 位移公式:s = ut + (1/2)at² (s为位移,u为初速度,t为时间,a为加速度)
4. 力学功公式:W = Fd (W为功,F为力,d为距离)
5. 动能公式:E = (1/2)mv² (E为动能,m为物体质量,v为速度)
6. 势能公式:E = mgh (E为势能,m为物体质量,g为重力加速度,h为高度)
7. 弹性势能公式:E = (1/2)kx² (E为弹性势能,k为弹簧常数,x为弹簧伸长量)
8. 万有引力定律:F = G(m₁m₂/r²) (F为引力,G为万有引力常数,m₁和m₂为物体的质量,r为物体之间的距离)
9. 牛顿第一定律:F = ma (F为力,m为物体质量,a为加速度)
10. 牛顿第二定律:F= ma (F为力,m为物体质量,a为加速度)
11. 牛顿第三定律:F₁ = -F₂ (F₁和F₂为相互作用的力)
12. 重力加速度公式:g = G(M/r²) (g为重力加速度,G为万有引力常数,M为地球质量,r为离地面的距离)
13. 简谐振动周期公式:T = 2π√(m/k) (T为振动周期,m为物体质量,k为弹簧劲度系数)
14. 矩阵乘法公式:C = AB (C为结果矩阵,A和B为相乘的矩阵)
15. 利用抛物线投射物体飞行时间公式:t = (2v₀sinθ)/g (t为飞行时间,v₀为初始速度,θ为发射角度,g为重力加速度)
16. 惯性力公式:F = -ma (F为惯性力,m为物体质量,a为加速度)
17. 摩擦力公式:F = μN (F为摩擦力,μ为摩擦系数,N为物体受力面的法向压力)
18. 波速公式:v = fλ (v为波速,f为频率,λ为波长)
19. 简单电路中电流与电压关系:I = V/R (I为电流,V为电压,R为电阻)
20. 电阻公式:R = ρl/A (R为电阻,ρ为电阻率,l为电阻长度,A为电阻横截面积)
21. 欧姆定律:U= IR (U为电压,I为电流,R为电阻)
22. 串联电阻公式:R = R₁ + R₂ + R₃ + ... (R为总电阻,R₁、R₂、R₃等为各个电阻的电阻值)
23. 并联电阻公式:1/R = 1/R₁ + 1/R₂ + 1/R₃ + ... (R为总电阻,R₁、R₂、R₃等为各个电阻的电阻值)
24. 电功率公式:P = IU(P为功率,I为电流,U为电压)
25. 能量守恒定律:E₁ + W = E₂ (E₁和E₂为起始和终止能量,W为外力做功)
26. 热传导公式:Q = kAtΔT/L (Q为传热量,k为热导率,A为传热面积,t为传热时间,ΔT为温度差,L为传热距离)
27. 热膨胀公式:ΔL = αL₀ΔT
数学板块
微积分
微积分是数学中的一个重要分支,研究的对象是函数的变化和极限。它是现代数学的基石之一,也是自然科学和工程科学的基础。
微积分的定义可以从两个方面来解释。
一方面,微积分可以被理解为对函数的“微分”和“积分”两个操作的研究。微分是研究函数在某一点的变化率或斜率,而积分则是研究函数的在某一区间上的面积或积累效应。
另一方面,微积分还可以被理解为数学中最基本的概念,包括极限、连续性和导数等。微积分的概念和内容源自于古代希腊数学中“方法论”的思想,而现代微积分的奠基人被认为是牛顿和莱布尼茨。牛顿和莱布尼茨几乎同时独立地发展了微积分的理论和方法,他们的贡献被称为“牛顿-莱布尼茨微积分”。
微积分的主要内容包括以下几个方面:1. 极限:微积分的核心概念之一是极限。极限可以理解为函数在无限接近某一点时的趋势或趋近于某一值的过程。例如,函数f(x)在x=a处的极限可以表示为lim(x→a) f(x) = L,其中L为函数f(x)在x=a处的极限值。通过研究极限,我们可以了解函数在某一点的性质和趋势。
2. 连续性:一个函数在某一点上连续,表示函数在该点处的极限存在且与函数在该点处的函数值相等。连续性是微积分中的重要性质,它决定了函数的可导性和可积性。对于连续函数,我们可以使用微积分的方法来研究其性质。
3. 导数:导数是微积分中的重要概念,它表示函数在某一点上的变化率或斜率。导数可以通过求取函数的极限来计算,表示为f'(x),也可以表示为dy/dx。导数可以用于描述函数的切线和切线的斜率,进而研究函数的增减性和极值点。
4. 积分:积分是微积分的另一个重要概念,它表示函数在某一区间上的面积或积累效应。积分的符号表示为∫,可以看作是导数的逆运算。不同于求导主要关注函数的变化积分关注的是函数的累积效应。积分可以求解函数的定积分和不定积分两种形式。
- 定积分:定积分表示函数在某一区间上的面积。定积分的计算可以通过将区间划分成无穷小的小矩形,并求和这些矩形的面积来进行近似计算。当小矩形的数量趋近于无穷大,并且划分足够细致时,得到的近似值就是定积分的精确值。定积分通常表示为∫f(x) dx,其中f(x)是被积函数,dx表示对x的积分变量。定积分可以用来计算函数的面积、曲线与坐标轴之间的面积、某一物理量的累积效应等。- 不定积分:不定积分表示函数的原函数或反导函数。
不定积分通常表示为∫f(x) dx = F(x) + C,其中F(x)是函数f(x)的一个原函数,C为任意常数。不定积分与定积分正好相反,其实际上是对导数的逆运算。不定积分可以用来解决函数的原始形式和求出曲线的方程。
5. 应用:微积分在自然科学和工程科学中具有广泛的应用。
例题:1. 求函数 $f(x)=3x^2-2x+1$ 在区间 $[-1,2]$ 上的定积分。解析:首先对函数 $f(x)$ 关于 $x$ 进行求导得到 $f'(x)=6x-2$。然后求出函数的原函数 $F(x)$,即 $F'(x)=f(x)$。通过积分公式可以求解得到 $F(x)=x^3-x^2+x+C$,其中 $C$ 为任意常数。接下来利用定积分的性质,有$$int_{-1}^{2} f(x) , dx = F(2)-F(-1) = (2^3-2^2+2)-((-1)^3-(-1)^2+(-1)) = 9.$$所以,函数 $f(x)=3x^2-2x+1$ 在区间 $[-1,2]$ 上的定积分为 9。
拓展:微积分是数学的一个重要分支,其中定积分是微积分的核心概念之一。它在量化描述变化的过程和计算面积、体积等问题中起到重要的作用。微积分在物理、工程、经济等领域具有广泛的应加速度的关系、曲线的切线与法线、最优化问题等。微积分的基本概念包括导数和积分,导数描述了函数在某一点的变化率,积分则是函数在某一区间上的累积效应。微积分的理论基础由牛顿和莱布尼兹等人建立,为数学分析学的核心内容。
总结:微积分是研究变化和累积效应的数学分支,其中定积分是其中重要的概念之一。可以通过求导和求积分解决物理、工程等相关问题。学习微积分需要掌握导数和积分的基本概念、性质和计算方法,并进行大量的例题练习来提高对微积分的理解和运用能力。
质数定理
质数定理是数论中的一个重要定理,它给出了非常接近于n的质数个数的估计。
定义:质数定理指出,对于任意正整数n,小于等于n的质数的个数大约为n/ln(n),其中ln(n)表示n的自然对数。
来源:质数定理最早是由法国数学家欧仁·查理·卡普利亚尼(Eugène Charles Catalan)在1846年提出,并且是后来被法国数学家雅克·欧卡尔姆(Jacques Charles François Sturm)和德国数学家埃尔兰根德·德德金(Carl Gustav Jacob Jacobi)证明的。
例题:求小于等于100的质数个数的近似值。
解析:根据质数定理,最接近100的质数个数约为100/ln(100) ≈ 100/4.605 ≈ 21.71。因此,小于等于100的质数个数的近似值为22。
拓展:1. 贝塞尔定理:贝塞尔定理是质数定理的一个拓展,给出了更精确贝塞尔定理是质数定理的一个拓展,通过添加一项关于误差项的校正,给出了更精确的质数个数的估计。贝塞尔定理的表述如下:对于任意正整数n,小于等于n的质数的个数Pi(n)满足以下不等式关系:Li(n) - θ(n) < Pi(n) < li(n) + θ(n)其中,Li(n)是庞加莱猜想中的对数积分函数,li(n)是原始对数函数(原始对数函数表示小于或等于n的质数个数的近似值),θ(n)是误差项。
总结:质数定理是数论中一个重要的定理,它给出了小于等于n的质数个数的近似值,即n/ln(n)。贝塞尔定理则是对质数定理进行了拓展,给出了更精确的质数个数的估计,并添加了误差项。质数定理及其拓展对于研究与质数相关的问题具有重要的理论意义和实际应用价值。
泰勒公式
泰勒公式来源:泰勒公式来源于数学家布鲁诺·波瓦洛夫斯基和格里戈里·泰勒的工作。他们在18世纪中期独立发现了这个公式,并使用它来近似计算各种函数的值。
泰勒公式定义:泰勒公式是一个用于将一个函数在某个点附近进行无穷次可导展开的公式。这个公式通过使用函数在该点及其导数的信息来逼近函数在该点附近的值。
泰勒公式内容:泰勒公式可以表示为以下形式:f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...其中,f(x) 是需要近似的函数,a 是展开点,f'(a)、f''(a)、f'''(a)分别代表 f(x) 在 a 点的一阶导数、二阶导数和三阶导数,以此类推。
泰勒公式例题:例如,考虑函数 f(x) = sin(x) 在展开点 a = 0 处的泰勒级数展开。展开到 n 阶的问题可以表示为以下形式:f(xf(x) ≈ f(0) + f'(0)(x-0) + f''(0)(x-0)^2/2! + f'''(0)(x-0)^3/3! + ... + f^(n)(0)(x-0)^n/n!要计算具体的展开式,需要求出 f(x) 在展开点 a = 0 处的各阶导数。f(x) = sin(x)f'(x) = cos(x)f''(x) = -sin(x)f'''(x) = -cos(x)...代入展开公式,可以得到:sin(x) ≈ x - x^3/3! + x^5/5! - x^7/7! + ...
泰勒公式解析:泰勒公式的核心思想是通过函数的各阶导数来近似计算函数在展开点附近的值。公式通过逐渐增加阶数,可以得到更精确的近似结果。当阶数趋于无穷时,泰勒公式收敛于原函数。
泰勒公式拓展:泰勒公式还可以进行多维展开,即针对多变量函数的展开。这被称为多元泰勒公式,通过对每个变量进行泰勒展开,可以得到函数在展开点附近的多项式近似。
泰勒公式总结:泰勒公式是一种用于近似计算函数值的重要工具。它可以通过使用函数在展开点附近的导数信息,将函数展开为一个无限级数。通过增加展开阶数,可以获得更精确的近似结果。泰勒公式在数学分析、物理学和工程学等领域有广泛应用,用于解决各种近似计算的问题。
欧拉公式
欧拉公式(Euler's formula)来源于瑞士数学家欧拉(Leonhard Euler)在18世纪提出。这个公式是关于复数(complex numbers)的一种表示方式。
定义:欧拉公式表述为:e^ix = cos(x) + i * sin(x),其中e是自然对数的底数(约等于2.71828),i是虚数单位(满足i^2 = -1),x是一个实数。
内容:欧拉公式表示了复数的极坐标形式。它将一个复数表示为以底数为e的指数函数和三角函数的和。具体地,左边的e^ix 被拆分成了它的实部cos(x) 和虚部sin(x)。
例题:例如,当x = π时,欧拉公式变为e^iπ = cos(π) + i * sin(π)。化简后得到e^iπ = -1。
解析:欧拉公式的解析解释可以从复数的泰勒级数(Taylor series)扩展来理解。泰勒级数可以将某个函数表示为无限多项的和,其中每一项都是函数的导数在某个点的值。通过将指数函数(exponential function)和三角函数在x = 0点处的泰勒级数展开,我们可以得到欧拉公式。
拓展:欧拉公式的拓展形式是欧拉公式的一般解,也称为欧拉恒等式(Euler's identity)。它是将欧拉公式中的x替换为π的倍数得到的结果:e^iπ + 1 = 0。
总结:欧拉公式将复数的极坐标形式表示为指数函数和三角函数的和。它是数学中重要的公式之一,可以用于解决与复数、三角函数和指数函数相关的问题。欧拉公式的拓展形式是欧拉恒等式,即e^iπ + 1 = 0。
对数函数
对数函数是指以某个固定正数为底的指数函数,它是指数函数的逆运算。对数函数的起源可以追溯到17世纪,当时数学家约翰·纳皮尔斯(John Napier)首先提出了对数的概念。对数函数的定义为:对于任意正实数x和正实数a(a≠1),记作logₐx,其中a被称为底数,x被称为真数。
定义中的对数函数满足一个基本性质:logₐaⁿ = n,其中n为实数。对数函数的内容包括底数、真数和对数值。底数a决定了对数函数的特性,常见的底数有10(常用对数)、e(自然对数)和2(二进制对数)。真数x是对数函数中的自变量,代表了要求对数的值。对数值则是对数函数的函数值,表示真数x在以底数a为底的对数中的结果。
下面是一个例题:已知log₈(2x + 1) = 3,求x的值。
解析:根据对数的定义,可将该方程转化为8³ = 2x + 1,解得x = 255.5
对数函数的拓展可以包括对数函数的性质、图像、应用等。例如,可以拓展对数函数的性质方面,包括对数函数的定义域、值域、增减性、奇偶性等。还可以探讨对数函数的图像,了解底数不同对图像的影响。对数函数在实际生活中也有广泛应用,如在解决指数增长问题、计算物质衰减、解决复利问题等方面。
总结起来,对数函数是指以某个固定正数为底的指数函数,起源于17世纪的数学研究。其内容包括底数、真数和对数值。解对数方程时,需要运用对数的基本性质。对数函数还可以拓展其性质、图像、应用等方面。对数函数在解决实际问题中有着广泛的应用。
威尔逊定理
威尔逊定理是一个关于素数的定理,它表明:如果一个正整数 p 是素数,那么 (p-1)!+1 能够整除 p。
这个定理最早由数学家威尔逊在1770年提出,并于1771年发表了证明。威尔逊利用排列组合的思想证明了这个定理。
例题:证明 23 是一个素数。
解析:根据威尔逊定理,我们需要证明 (23-1)! + 1 能够整除 23。计算 (23-1)!,得到 22! = 1 * 2 * 3 * ... * 22。计算 (23-1)! + 1,得到 22! + 1。计算 (23-1)! + 1 对 23 取余,得到 22! + 1 ≡ 0 (mod 23)。所以,(23-1)! + 1 能够整除 23,因此 23 是一个素数。
拓展:威尔逊定理的应用主要在素数的判定中。对于一个较小的数可以通过计算 (p-1)! + 1 是否能够整除 p 来判断其是否为素数。然而,随着数值的增大,计算 (p威尔逊定理的拓展应用还包括在密码学中。基于威尔逊定理的原理,可以构建一种称为威尔逊素性测试的算法。这个算法可以在较快的时间内判断一个给定的数是否为素数。然而,由于计算 (p-1)! 可能涉及大数运算,导致时间复杂度较高,因此在实际应用中往往会使用更高效的算法,如米勒-拉宾素性测试。
总结:威尔逊定理是关于素数的一个定理,它表明如果一个正整数 p 是素数,那么 (p-1)!+1 能够整除 p。威尔逊定理最早由威尔逊在1770年提出,并在1771年发表了证明。威尔逊定理可以用于素数的判定,但在实际应用中往往会使用更高效的算法。此外,威尔逊定理还有拓展应用在密码学领域。
中国剩余定理
中国剩余定理(Chinese Remainder Theorem)是一种数论中的重要定理,它可以用来解决一组线性同余方程的问题。
该定理最早由中国的数学家孙子在《孙子算经》中提出,因此得名为中国剩余定理。
中国剩余定理的基本形式为:对于任意给定的正整数m1, m2, ..., mn,它们两两互素并且大于1,以及任意给定的整数a1, a2, ..., an,那么对于任意整数M,以下方程组有解且解唯一:x ≡ a1 (mod m1)x ≡ a2 (mod m2)...x ≡ an (mod mn)其中x是解,M是模数,即x是对于模数为M的一个解。
例题:解方程组:x ≡ 2 (mod 3)x ≡ 3 (mod 5)x ≡ 2 (mod 7)
解析:根据中国剩余定理,令M = m1 * m2 * m3 = 3 * 5 * 7 = 105,a1 = 2,a2 = 3,a3 =2。然后求解模M下的逆元,即对于每个mi,求Mi,使得Mi ≡ M/mi (mod mi)。在这个例子中,我们有3个模数,求解它们的逆元:M1 = M/m1 = 105/3 = 35M2 = M/m2 = 105/5 = 21M3 = M/m3 = 105/7 = 15接下来,我们需要求解每个方程的解,即对于每个mi,求解xi,使得xi * Mi ≡ 1 (mod mi)。对于mi = 3,有 xi * 35 ≡ 1 (mod 3)。通过求解这个方程,我们得到xi = 2。对于mi = 5,有 xi * 21 ≡ 1 (mod 5)。通过求解这个方程,我们得到xi = 1。对于mi = 7,有 xi * 15 ≡ 1 (mod 7)。通过求解这个方程,我们得到xi = 1。最后,我们可以得到x = a1 * M1 * x1 + a2 * M2 * x2 + a3 * M3 * x3 = 2 * 35 * 2 + 3 * 21 * 1 + 2 * 15 * 1 = 233。所以方程组的解为x ≡ 233 (mod 105)。
拓展:中国剩余定理不仅适用于两个模数的情况,也可以适用于多个模数的情况。具体的步骤类似于上述例题的解法,只是需要求解更多方程和逆元。
总结:中国剩余定理是一种用于解决线性同余方程组的定理,可以将原问题转化为求解多个模数的方程的解。它的应用领域广泛,例如在密码学、计算机科学、编码和解码等领域都有重要的应用。
高斯函数
高斯函数是一种常见的数学函数,也称为正态分布函数或钟形曲线函数。
高斯函数的拓展公式包括:
1. 一维高斯函数
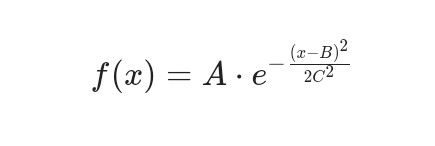
2. 二维高斯函数
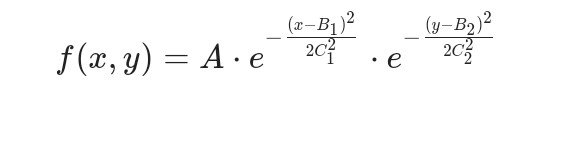
3.多维高斯函数
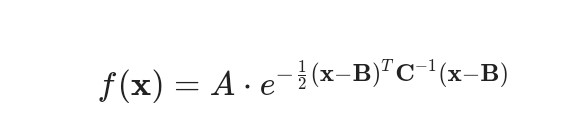
5. 带有平移和缩放的一维高斯函数
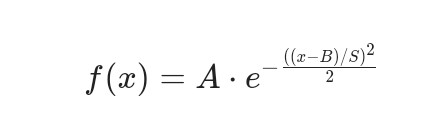
来源:高斯函数最早由德国数学家高斯(Carl Friedrich Gauss)在统计学领域中引入和研究,用于表示实际测量值的分布情况。高斯函数在自然界和科学研究中广泛应用。
拓展:1. 高斯函数可以用于描述连续型随机变量的概率分布,其曲线呈钟形。在统计学中,高斯函数常被用于拟合实际观测到的数据,以求得数据的均值和标准差。
2. 高斯函数具有对称性,即关于均值 ( mu ) 对称。它的均值决定了曲线的中心位置,而标准差决定了曲线的宽窄程度。3. 高斯函数是数学中的一种特殊函数类型,其形式简洁且具有很多重要性质。因此,在各个科学领域和工程应用中,高斯函数经常被采用来建立模型、分析数据和做出预测。
总结:高斯函数是一种常见的数学函数,用于描述实际测量值的分布情况。它具有对称性,中心位置由均值决定,分布的宽窄程度由标准差决定。

素数分布定理
素数分布定理(Prime Number Theorem)是数论中的一个重要定理,描述了素数在自然数中的分布规律。
具体来说,素数分布定理表明当自然数n趋向无穷时,小于等于n的素数的个数近似等于n / ln(n)。
这个定理最早由法国数学家雅各布·伯努利(Jacques Bernoulli)在18世纪初提出,随后由独立工作的欧拉和格里姆为其提供了更完整的证明。 最后,在19世纪初,德国数学家哥德巴赫(Carl Friedrich Gauss)进一步加强和完善了该定理的证明。
下面是一个素数分布定理的例题:例题:证明当n趋向无穷时,小于等于n的素数的个数近似等于n / ln(n)。
解析:要证明素数分布定理,需要使用复杂的分析数论工具和技巧,超出了一般高中水平的数学知识。证明细节较为复杂,需要使用一系列数学方法和技巧,包括复变函数论、泰勒展开、复数解析性质等。
具体证明过程可以在数论专业的教材或研究文献拓展:素数分布定理的证明过程非常复杂,在数学领域有着重要的地位。在此基础上,还有一些相关的拓展理论,包括但不限于:
1. 素数间隔猜想(Twin Prime Conjecture):猜想存在无穷多对相差为2的素数(例如3和5、11和13等)。这个猜想虽然没有得到证明,但被广泛认为是真实的。
2. 周期性的素数分布问题:研究素数分布中的一些周期性现象,如素数的末尾数字的分布规律、质数数列中连续素数之间的间隔分布等。
3. Riemann猜想(Riemann Hypothesis):提出于1859年的著名猜想,关于复数平面上的黎曼ζ函数的非平凡零点的位置。这个猜想与素数分布有着密切的关系,因为它能够提供关于素数分布的更加精确的信息。
总结:素数分布定理揭示了素数在自然数中的分布规律,是数论中的一个重要定理。这个定理的证明相当复杂,需要使用复杂的分析数论工具。
以下是一些被认为非常困难的数学难题:
1. 著名的哥德巴赫猜想:是否对于任意大于2的偶数都存在两个质数之和。迄今为止,尽管有很多人尝试解决这个问题,但尚未找到确定的解答。
2. 弗雷曼贝克猜想:该猜想是在无线平面上的单位圆,是否存在一个包含无限个点的集合,使得这些点的最小距离大于1。目前对于这个问题还没有确切的答案。
3. P与NP问题: 这是计算机科学中一个重要的问题,涉及是否存在一种有效的算法去解决一个问题,并且可以在多项式时间内验证答案的正确性。尽管有很多人在研究这个问题,但还没有找到确定的解答。
4. 纳什均衡:这是在博弈论中的概念,涉及到多个参与方在给定策略下,无法通过单方面改变策略来获得更好结果。尽管理论上存在这样的均衡尽管理员论上存在这样的均衡点,但在实际情况下,找到并证明均衡点的存在性和性质仍然是一个非常困难的问题。
高等数论
1. 素数分布定理:素数在自然数中的分布规律。素数定理表明,在自然数n趋向无穷时,小于等于n的素数的个数近似等于n/ln(n)。
2. 埃拉托色尼筛法:一种用于筛选素数的方法。通过不断排除素数的倍数,可以找到给定范围内所有的素数。
3. 约数函数和分割函数:约数函数d(n)表示正整数n的约数个数,分割函数p(n)表示将n分割成整数之和的方式数目。这两个函数在高等数论中具有重要的应用。
4. 质数定理:描述素数分布的一个更精确的定理。质数定理给出了当n趋向无穷时,小于等于n的素数的个数与n/ln(n)的差异的上界和下界。
5. 素数元素周期表:通过将素数按照一定规则排列,可以观察到一些规律和周期性现象。素数元素周期表是高等数论中的一个重要研究工具。









