数学

格点行走问题——无穷期望问题的线性递推方法与思考

注:本帖中的问题难度均不高，却有一定的价值，老少咸宜……

我们先提出一个最简单的问题，找到求解方法，再尝试推广，这是数学问题的很好研究方法。

解:第一步必然走到左上角或右下角，第二步有1/2概率走到终点，有1/2的概率回到起点。而若回到起点，则重复上面的过程，如此我们便得到期望$E=\sum_{k=1}^\infty \dfrac{2k}{2^k}=4$

请自行思考一下

这个问题就稍具难度了，想分类讨论无穷求和似乎非常困难，既然求不出来，那干脆就不求了吧！

……

好吧，开个玩笑，当然问题还是要解决的。所谓“不求了”不是放弃这个问题，而是不去直接求解，只找出一些递推关系。

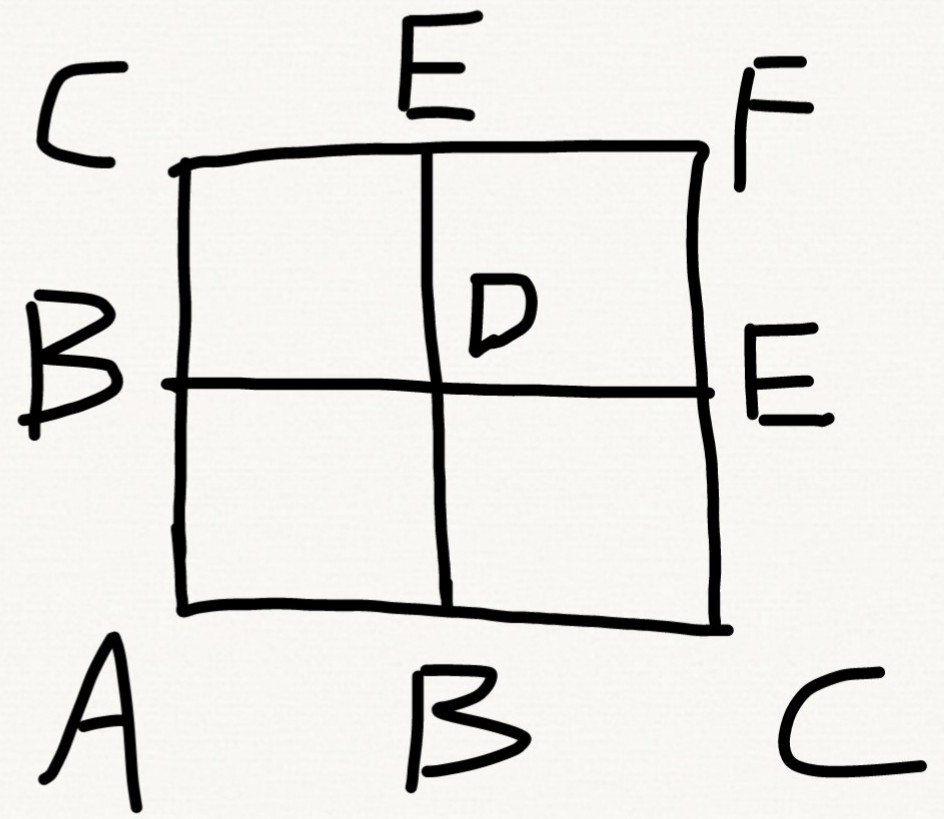
解:将图形中的点标上字母，由图形的对称性，我们把对称的点标为同一字母，方便计算。

我们记$E_A$为从A点走到F点的路程期望，$E_B$为从B点走到F点的路程期望，同理地，定义$E_C$，$E_D$，$E_E$，$E_F$

注意到$E_A$和$E_B$之间是有很紧密的联系的，从A点必定会一步走到B点，而此时的期望就从$E_A$变成了$E_B$

于是我们得到了第一个递推关系式:$E_A=E_B+1$

同理地，$E_B$与$E_A$，$E_D$，$E_C$之间也都有联系，从B点一步走到A点，C点，D点的概率均为$\dfrac{1}{3}$于是我们得到了第二个递推关系式:$E_B=\dfrac{1}{3}(E_A+1)+\dfrac{1}{3}(E_C+1)+\dfrac{1}{3}(E_D+1)$

同理地列出其他递推关系式，它们会组成线性方程组:

$\begin{cases}E_A=E_B+1\\E_B=\dfrac{1}{3}(E_A+E_C+E_D)+1\\\\E_C=\dfrac{1}{2}(E_B+E_E)+1\\\\E_D=\dfrac{1}{2}(E_B+E_E)+1\\\\E_E=\dfrac{1}{3}(E_C+E_D+E_F)+1\\\\E_F=0\end{cases}$

求解即得$E_A=8$

其实我们还可以把这个方程组理解成:由$E_F=0$这一显然条件，一步步与其他点线性递推，直至推出$E_A$

回到问题1，我们可以用同样的方法

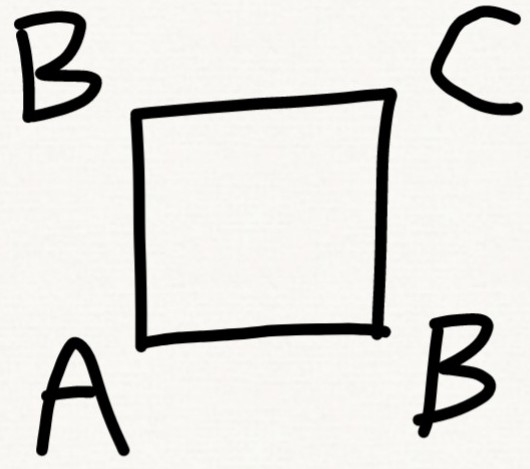
$\begin{cases}E_A=E_B+1\\E_B=\dfrac{1}{2}(E_A+E_C)+1\\E_C=0\end{cases}$

同样解得$E_A=4$

我们仅仅用了一个线性方程组就解决了它，是不是比无穷级数求和的办法简单多了呢？

其实，网格根本不必是正方形的，无论给出的网格多丑，我们都能用此办法解决。从而我们解决了任意形状的有限格点行走问题。

不过，我们当然不能止步于此，我们需要尝试继续将它应用在其他的无穷期望问题中。

下面是一道北大自招原题。

此题用一般方法来做，思维量和计算量均不小，但用前文介绍的方法，我们可以秒杀它。

解:记$E_k$为此次抛掷前已连续出现$k$次正面，还需抛掷的次数期望。

我们有$\begin{cases}E_0=\dfrac{1}{2}(E_0+E_1)+1\\\\E_1=\dfrac{1}{2}(E_0+E_2)+1\\\\E_2=\dfrac{1}{2}(E_0+E_3)+1\\\\E_3=\dfrac{1}{2}(E_0+E_4)+1\\\\E_4=0\end{cases}$

解得$E_0=30$，即为所求期望。

同样的，我们也可以把这个方程组理解成由$E_4=0$这一显然条件向前线性递推得到$E_0$

结语:篇幅有限，暂时只能介绍这三个问题了。无穷期望问题在各大学的强基与各种自招考试中出现频率较高，还是有必要了解掌握的。

通过这种线性递推的方法，我们可以秒杀绝大部分的无穷期望问题。但是是否能对此方法再做改进，或者找出更好的求解方法呢？答案尚未可知，帖主也还在探索中，大家也可以自行研究。

最后，对一些问题进行征解，望读者积极挑战！将答案回复在本帖下即可。