物理

[长更新]物竞解题小技巧(全系列)

[10.08已更新 正则角动量]

2023.09.08

今日主角——pV曲线最值问题

如图，求直线AB过程中的最高温度

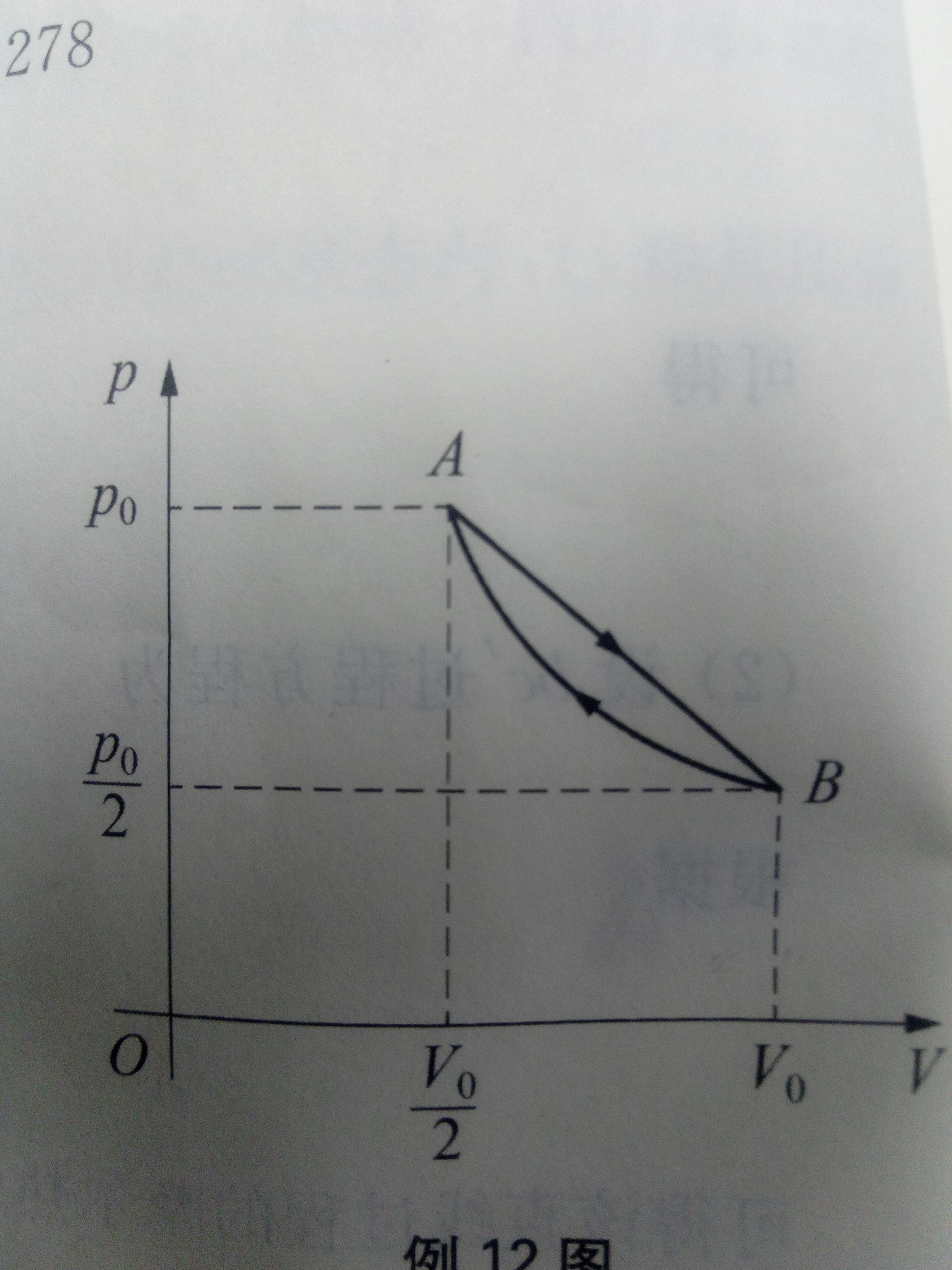
思路一:考虑压强体积线性方程与理想气体状态方程联立，得到二次非线性方程

即p=3/2p₀-p₀V/V₀

pV=nRT

联立得到T关于V的二次方程求极值即可。

这种方法思路简明，缺点是计算量稍大。

思路二:考虑理想气体准静态过程的一般摩尔热容变化

即除Cv和Cp外更普遍的理想气体摩尔热容，用Cm表示

在任意缓慢变化中，根据热力学第一定律，有:

δQ=CmdT，δW=-pdV，dU=CvdT，又有克拉珀龙方程，得:

pdV/dT+Vdp/dV·dV/dT=R，之所以要求T对V的微商，是为后边过程凑出dQ行方便

根据上式，就有dV/dT=R/(p+Vdp/dV)，再带入初始条件就可以得到Cm与Cv的关系。

根据该关系，我们可以得到Cm与体积的单一变量关系，又由于摩尔热容的定义:

C=δQ/δT

可以分别求出吸热量和温度的最值以及拐点。

这种方法缺点很明显，思维量比较大，当然优势也很突出——结论万金油属性强，对理清思路，拓展背景有不小帮助。

总结:对于多方过程曲线的最值问题，通常以克拉珀龙方程和pV线性方程为基础解题，同时辅助以其他物理量例如摩尔热容和其他基本方程如热一定律。

2023.09.09

今日主角——妙解纯滚

纯滚问题是刚体中常考的问题，也是很能体现刚体力学特点的问题。

你还在为找不到线速度和质心速度的关系而烦恼吗？今天给大家提供一种新的思路。

我们以第37届复赛第二题第一小问为例，如图:

首先最基本的常规操作，冲量定理求质心速度，刚体角动量定理求接触点线速度，即:

P=mVc

J=P·R/2

J=Iω₀-0

I=2/5mv²

Va=Vc-ωR

可以解得Va，并且容易知道它是一个负值，那么摩擦力显然朝右，有:

f=-mgμ=Iβ

ma=-μmg

根据上式以及基本的运动学公式很容易得到质心速度，母球角速度，以及接触点线速度与时间的关系，最后当且仅当:

Va(t)=0时，解得:

t=P/14μmg，Vc'=15P/14m

总结:纯滚问题可以说是刚体中最有套路题型的典型代表之一，掌握它并不难，只需要一些基本的公式如三定理两守恒，但纯滚问题的花样变换却不少，因此为了在复赛考场上节省更多时间，在这类基础题型的妙解上下功夫是必要的。

2023.10.04

今日主角——正则动量

正则顾名思义，与正交垂直有关，在处理一些与轴矢量（赝矢量）相关的运动问题中能发挥出“于万军中斩敌将首级，如探囊取物耳”的神奇功效。比较典型的例子就是带电粒子在磁场中的运动，能将众多压轴题秒杀。

首先它的诞生或者推导就令人感到既在意料之外，又在情理之中。

以洛伦兹力为例，带电量为q，质量为m的电荷在磁感应强度为B的磁场中，满足如下等式

ma=qv×B，考虑最简单的情况，速度矢量与磁感应强度矢量相互垂直，则有

ma=qvB

两边同时对时间积分，有

∫ma dt=∫qBv dt

即mv=qBx+C，显然当v=0时有x=0，故C=0

即mv=qBx，即在轴矢量场中，物体运动的速度跟位移成正比。怎么样神奇吧^_^

接下来还有更神奇的，假如在直角坐标系xOy中对速度和位移进行正交分解，此时轴矢量即z轴上的矢量

那么有mVx=qBy，mVy=qBx

文字表述为，在轴矢量场中，速度的x分量由位移的y分量决定，速度的y分量由位移的x分量决定。

话不多说，直接上题:

这道题初看无从下手，复看眉头深皱，再看浑身发抖。正则动量一学，随便儿就有。

解题如下:

首先它是一个轴矢量场，很明显是可以用正则动量来做的。不过这里有一个小变化，

磁场是随y方向的位移而变化的（会导致积分的时候出现一点小插曲），那么由于x具有平移对称性，我们就算x方向的速度。

即max=qVyB=qVy αy，积个分得到:

mVx=αy² q/2 即x方向正则动量守恒。

当粒子运动到y方向最远的时候，有ym=h，Vy=0，Vx=V₀

再简简单单列一个能量守恒，有mV₀²/2=Eqh

又mV₀=αh²/2，联立可得。

总结:正则动量守恒本质上是由物体的平移对称性决定的，一切守恒量都与对称性有关。例如角动量守恒与旋转对称性有关，能量守恒与时间对称性有关，动量与平移对称性有关，正则动量实际上是特殊场中的特殊动量，不影响它与平行对称性的联系。

2023.10.08

今日主角:正则角动量

上期我们讲了正则动量，其本质是平移对称性的体现，今天推而广之，来讲一讲旋转对称性的体现——正则角动量。

如果存在一个圆形的磁场，磁感应强度的方向垂直于纸面向内，很显然，磁场具有旋转对称性。如果有一个粒子质量为m，电荷量为q，且在磁场中有竖直向上的速度v。

那么其角向磁场力及径向磁场力分别为

FΘ=qBVr，Fr=-qBVΘ

列角动量定理可得

FΘ r dt=dL=d(mrVΘ)

即qBVr dt r=d（mrVΘ）⇨qBr dr=d（mrVΘ）⇨d（mrVΘ-1/2qBr²）=0

即mrVΘ-1/2qBr²=0，角向的速度与径向的位移成正比，且二者的差为零，是一个守恒量。

这就是竞赛中也很常用的正则角动量守恒。

我们来考虑这样一个问题。一个实心圆柱导体和一个中空的圆柱形导体共轴放置，其间为真空，内柱半径为a，外柱半径为b，外层电视比内层高V,有匀强磁场B平行于轴指向纸面外。

问题1，若加入一个电子到不了外侧，离轴心最远处为Rm，试求到达这个距离时电子的速率v。

问题2，若增加B到一个值Bc，使得内柱表面无初速度溢出的电子不能到达外柱，求Bc。

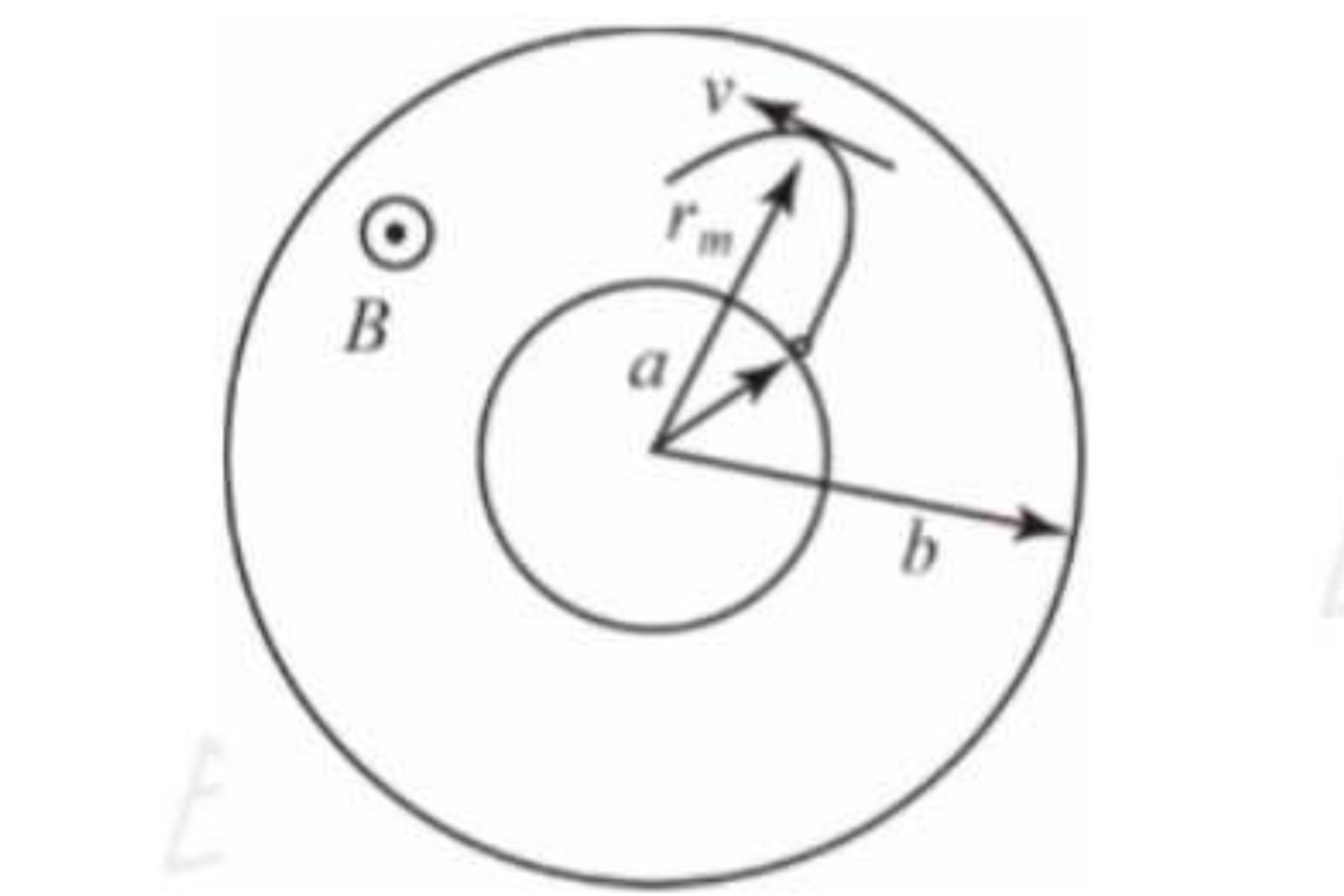
根据正则角动量守恒，起初无初速度， 末速度为v，则有：

-mvRm+1/2qBRm²=1/2qBa²

-mVΘr-1/2qBb²=1/2qBa²

又能量守恒：1/2mv²=qv

即可得结果。

我们通过一个简单的例题告诉大家正则角动量的产生及其应用。和之前所讲的正则动量类似，粒子在场中的受力都不是耗散力，所以我们对整个物理过程具有时间反演对称性，于是存在能量守恒。

用一句话总结就是：对称性产生守恒量！