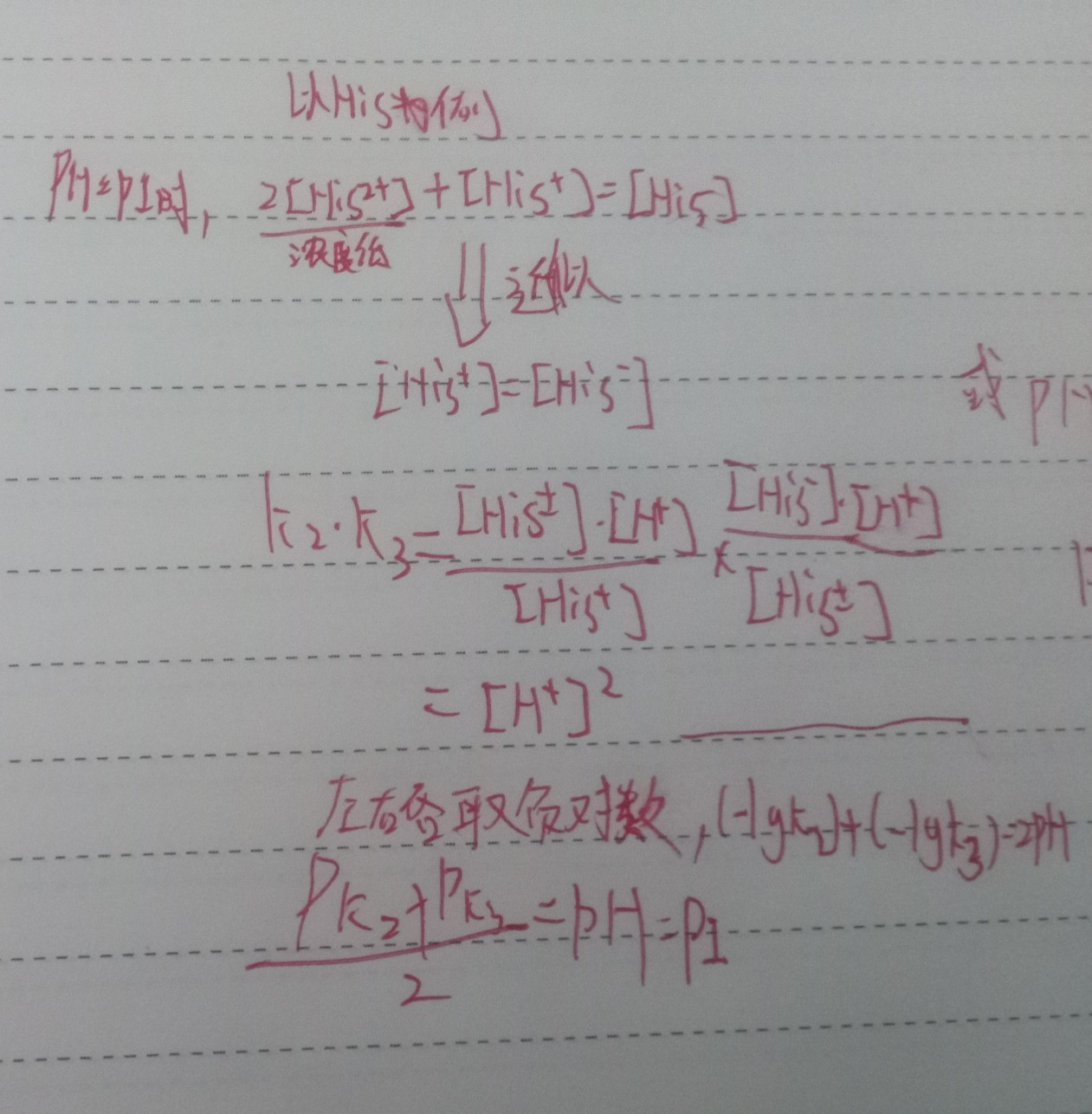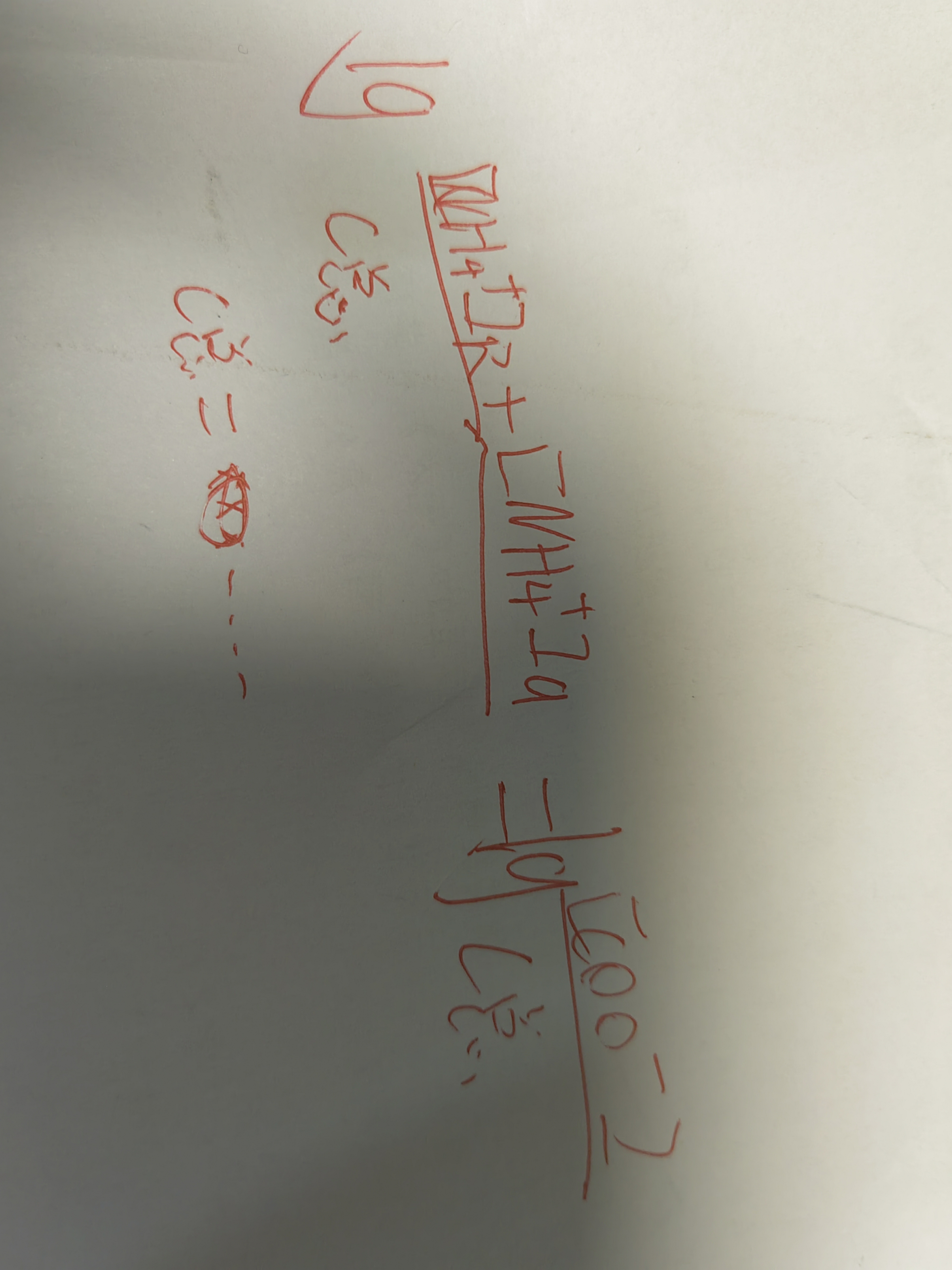化学 疑惑的后续
2023.10.2
经过进一步学习，最近又发现HH方程是可以直接由定义式导出来的，所以疑惑其实还没有解决（现在我的推测是PH本身的定义问题，在过算或过碱环境下离子积常数失效，PH失去意义）
（负号已加）
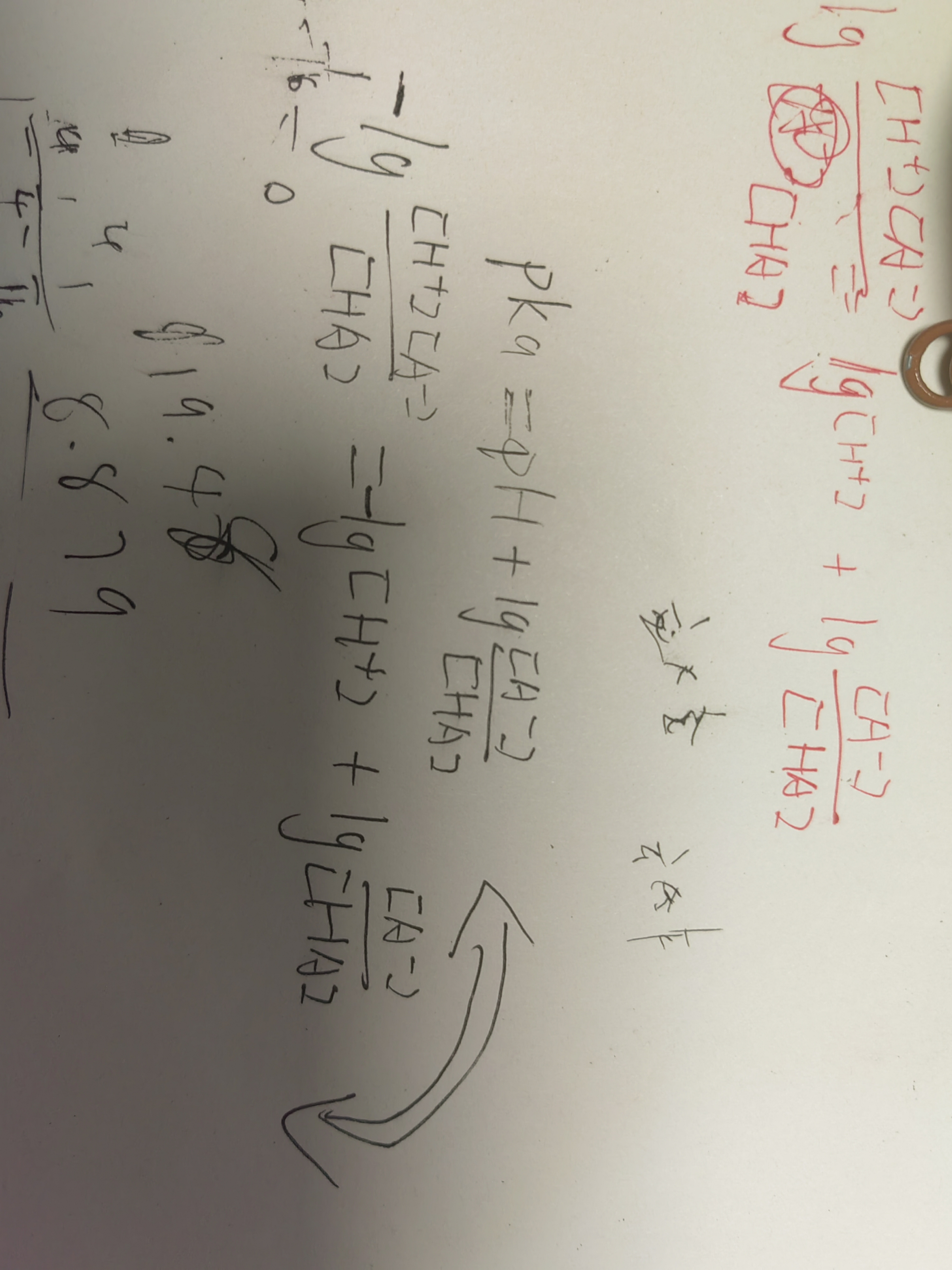
（@G&K 佬貌似不见好久了。。。有机会回来一定要看看啊！！！）
2023.8.31
该疑惑已解决，感谢@G&K 的解答，点醒了我
我对这个东西其实完全是零基础（课内连平衡常数都还没教），在此之前更不知道居然已经有专门的学科在研究这个，连物料守恒之类的名词也完全没听过，整个推导完全是我看到一个“近似式”而产生的灵感，想用数学来解决我对生物中等电点计算过程简略的不满。略微了解了一下这门学科才发现我多少有点初生牛犊不怕虎了，这个问题远远比我想象的要复杂。但至少，我知道我错在哪里了。
————————————
本来对这个问题的解释不报希望了，可发现还有人在看那个帖子，为了避免别人受到误导，我决定还是把后续的发现放上来吧
之前那个帖子等电点是代入数据倒推的，用误差解释有一定作用，所以我决定正推
误差达到了0.27，这已经不算小了，并且还有两个解（原本的想法是两个解的误差都小到一定程度就可以忽略了）
貌似有机化学里也有相同的内容，我期待化学区能给我一个满意的回答
下面说说，我得到的解释
1.③式应视为完全电离，该解是只考虑数学造成的后果
2.其实我能想到的最满意的解释是方程（共轭酸）那个由于某种原因不再适用，可以从这个角度出发
- 1
想了差不多一个小时 然后搞出来了个很麻烦的三元对数方程就推不下去了 这个公式只要是缓冲溶液就通用的 但是缓冲溶液必定满足1.溶液不稀和2.氢离子或氢氧根离子浓度都不接近原料浓度这两点 如果ph到了十几恐怕这对于蛋白质来说氢氧根浓度过高了 在我的那条公式下面也有解释的 原因就是在违反这两条规律时进行的一些近似处理会变得不精确 你可以尝试使用精确式或者分布分数进行计算 我看你的式子上是一串物料守恒和一个电荷守恒 还有三个针对等电点的方程 那应该还少一个方程才能防止增根 但是草稿纸下半部分我实在是看不懂 只能把自己的思路拿出来抛砖引玉
实在是麻烦你了，花了这么久，谢谢(´▽｀)ノ♪
那个精确式我不大看得懂，那几个K跟PKa是一个东西吗？能不能解释一下各项的含义
终于考完试了，我刚刚花时间详细看了看，终于算是明白一点点了。就是那个PKA那个方程是个近似方程，而如果采用精确式的话，我的整个思路相当于废掉了。。。精确式看着实在让人头痛，我得花时间好好想想它是怎么导出来的，再从其中找找思路
评论发不了图，放这了@G&K
具体哪步开始看不懂，下面就是一个变换，目的是凑出这个
C总，也就是你指的物料守恒，原因是这些基团全在一个氨基酸上，解离的和不解离的浓度和自然都等于氨基酸的浓度。
$[H^+],[OH^-]$是氢离子和氢氧根浓度
$C_A$是共轭酸的浓度 $C_B$是共轭碱浓度
$K_a$是这对酸碱对的平衡常数
p是负对数操作这个是常识
最下面的那个等式就是把左边取lg变成了右边
二基团的证明确实很显然，不然我也不会一开始就抛出三基团的问题了（）
我这边也快要讲到统计了小，得认真听，等下课可以去知识点聊聊你们中学啊
但是即使是三基团也只看两个啊，其中第一个在PH很小的时候就已经完全解离了，画钟形图基本就到x轴上了不做考虑
并且我从来没有见过三个基团同时在不完全解离状态的分子（即使化学），应该是很不稳定
（你好好上课吧先别回复我下课再说）
（今晚约了导，等晚一点如果可以我试着找你）
（但可能是很晚很晚如果你早睡就算了好好休息）
实际上严格的解只需要三个方程，一个pi的定义，以及各个物种浓度之比与质子浓度的关系就可以（好像没用到什么近似吧）
主要是总共三个基团，我这是试着在不忽略第三个基团的情况下，看看此情况下解和忽略差距到底大不大
忽略第三个基团就是近似处理啊
理论上pka差距只要大于二即可
嗯，我那天正是闲的蛋疼想去验证一下这个“理论”是否合理，误差是否能够忽视